【E資格対策】情報理論

自己情報量・相互情報量

自己情報量

自己情報量とは, ある一つの事象が起きたとき, その事象がどれほど起こりにくいかを表す尺度である. 自己情報量 I(A)I(A) は, 事象 AA の起きる確率 P(A)P(A) を用いて次のように定義される :

I(A)=−log⁡2P(A)I(A) = -\log_{2} P(A)

直感的には, 「ほとんど起こらない珍しい事象が起きたときに, 多くの情報量が得られる」と考えられる.

相互情報量

相互情報量とは, 二つの情報量 X,YX, Y が互いにどれだけ影響し合っているか(相互に共有しているか)を表す尺度であって, 各事象の確率の積と, それらの同時確率の比を用いて次のように定義される :

I(X;Y)=EP(x,y)[−log⁡2P(x)P(y)P(x,y)]=−∑x∈X∑y∈YP(x,y)log⁡2P(x)P(y)P(x,y)=∑x∈X∑y∈YP(x,y)log⁡2P(x,y)P(x)P(y)\begin{align*} I(X; Y) & = \mathbb{E}_{P(x, y)} \left[ -\log_{2} \frac{P(x)P(y)}{P(x, y)} \right] \\ & = - \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} \frac{P(x)P(y)}{P(x, y)} \\ & = \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} \frac{P(x, y)}{P(x)P(y)} \\ \end{align*}

2行目から3行目の式変形では, 対数の分子・分母の交換によって符号が反転していることに注意.

また、二つの事象 X,YX, Y 間に依存関係がないとき, P(x,y)=P(x)P(y)P(x, y) = P(x)P(y) となり, I=0I = 0 で最小値を取る.

エントロピー・条件付きエントロピー・結合エントロピー・クロスエントロピー

エントロピー(シャノン情報量)

エントロピーとは, 確率変数の各値の自己情報量の期待値として定義され, 平均情報量とも呼ばれる. 具体的には, 確率変数 XX のエントロピー H(X)H(X) は, 以下のように表される :

H(X)=−∑x∈XP(x)log⁡2P(x)H(X) = - \sum_{x \in X} P(x) \log_{2} P(x)

確率変数は連続でもよく, その場合は ∑\displaystyle \sum を ∫\displaystyle \int に置き換えることで計算できる.

また, 確率分布が一様である場合にエントロピーは最大となる.

条件付きエントロピー

条件付きエントロピーとは, ある確率変数 YY が既知である下で, 新たに確率変数 XX について知ったときに得られる情報量の期待値として定義される :

H(X∣Y)=EP(x,y)[I(X∣Y)]=∑x∈X∑y∈YP(x,y)I(x∣y)=−∑x∈X∑y∈YP(x,y)log⁡2P(x∣y)\begin{align*} H(X | Y) & = \mathbb{E}_{P(x, y)} \left[ I(X | Y) \right] \\ & = \sum_{x \in X} \sum_{y \in Y} P(x, y) I(x | y) \\ & = - \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} P(x | y) \end{align*}

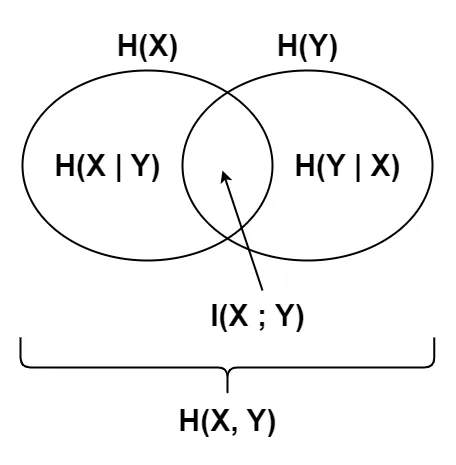
また、 H(X)H(X) を事前エントロピー, H(X∣Y)H(X | Y) を事後エントロピーとしたとき, 両者の差分である H(X)−H(X∣Y)H(X) - H(X | Y) は, 確率変数 YY によって得られる XX についての情報量の期待値を表し, これは相互情報量 I(X;Y)I(X; Y) と等しい :

H(X)−H(X∣Y)=I(X;Y)H(X) - H(X | Y) = I(X; Y)
証明 (クリックで展開) H(X)−H(X∣Y)=−∑x∈XP(x)log⁡2P(x)+∑x∈X∑y∈YP(x,y)log⁡2P(x∣y)=−∑x∈X∑y∈YP(x,y)log⁡2P(x)+∑x∈X∑y∈YP(x,y)log⁡2P(x∣y)=∑x∈X∑y∈YP(x,y)log⁡2P(x∣y)P(x)=∑x∈X∑y∈YP(x,y)log⁡2P(x,y)P(x)P(y)=I(X;Y)\begin{align*} H(X) - H(X | Y) & = - \sum_{x \in X} P(x) \log_{2} P(x) + \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} P(x | y) \\ & = - \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} P(x) + \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} P(x | y) \\ & = \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} \dfrac{P(x | y)}{P(x)} \\ & = \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} \dfrac{P(x, y)}{P(x)P(y)} \\ & = I(X; Y) \tag*{$\blacksquare$} \end{align*}

ここで, 1行目から2行目の変形に, 周辺確率の性質 : P(x)=∑y∈YP(x,y)P(x) = \displaystyle \sum_{y \in Y} P(x, y) を用いた.

結合エントロピー

結合エントロピーとは, 二つの確率変数 X,YX, Y の同時分布に基づくエントロピーとして定義される :

H(X,Y)=−∑x∈X∑y∈YP(x,y)log⁡2P(x,y)H(X, Y) = - \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} P(x, y)

また、以下のような関係式が成り立つ :

H(X,Y)=H(X)+H(Y)−I(X;Y)H(X, Y) = H(X) + H(Y) - I(X; Y)
証明 (クリックで展開) H(X,Y)=H(X)+H(Y)−I(X;Y)=−∑x∈XP(x)log⁡2P(x)−∑y∈YP(y)log⁡2P(y)−∑x∈X∑y∈YP(x,y)log⁡2P(x,y)P(x)P(y)=−∑x∈X∑y∈YP(x,y)log⁡2P(x)−∑x∈X∑y∈YP(x,y)log⁡2P(y)−∑x∈X∑y∈YP(x,y)(log⁡2P(x,y)−log⁡2P(x)−log⁡2P(y))=−∑x∈X∑y∈YP(x,y)log⁡2P(x,y)\begin{align*} H(X, Y) & = H(X) + H(Y) - I(X; Y) \\ & = - \sum_{x \in X} P(x) \log_{2} P(x) - \sum_{y \in Y} P(y) \log_{2} P(y) - \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} \frac{P(x, y)}{P(x)P(y)} \\ & = - \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} P(x) - \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} P(y) \\ & \quad - \sum_{x \in X} \sum_{y \in Y} P(x, y) \left( \log_{2} P(x, y) - \log_{2} P(x) - \log_{2} P(y) \right) \\ & = - \sum_{x \in X} \sum_{y \in Y} P(x, y) \log_{2} P(x, y) \tag*{$\blacksquare$} \end{align*}

エントロピーの関係図

クロスエントロピー

クロスエントロピーとは, ある確率分布 Q(X)Q(X) が基準となる確率 分布 P(X)P(X) からどれだけ離れているかを表す尺度であり, 次のように定義される :

H(P,Q)=−∑x∈XP(x)log⁡2Q(x)H(P, Q) = - \sum_{x \in X} P(x) \log_{2} Q(x)

P(X)=Q(X)P(X) = Q(X) のとき, クロスエントロピーは最小になる.

KLダイバージェンス・JSダイバージェンス

KL(Kullback-Leibler)ダイバージェンス

KLダイバージェンスは相対エントロピーとも呼ばれており, クロスエントロピーと同様に, ある確率分布 Q(X)Q(X) が基準となる確率分布 P(X)P(X) からどれだけ離れているかを表す尺度であり, 次のように定義される :

DKL(P∣∣Q)=∫xP(x)log⁡2P(x)Q(x)dxD_{KL}(P || Q) = \int_{x} P(x) \log_{2} \dfrac{P(x)}{Q(x)} \mathrm{d}x

KLダイバージェンスは対称性を持たないことに注意すること.

DKL(P∣∣Q)≠DKL(Q∣∣P)D_{KL}(P || Q) \neq D_{KL}(Q || P)

また, KLダイバージェンスは, クロスエントロピーとエントロピーの差に分解できる :

DKL(P∣∣Q)=∫xP(x)log⁡2P(x)Q(x)dx=−∫xP(x)(log⁡2Q(x)−log⁡2P(x))dx=−∫xP(x)log⁡2Q(x)dx−(−∫xP(x)log⁡2P(x)dx)=H(P,Q)−H(P)\begin{align*} D_{KL}(P || Q) & = \int_{x} P(x) \log_{2} \dfrac{P(x)}{Q(x)} \mathrm{d}x \\ & = -\int_{x} P(x) \left( \log_{2} Q(x) - \log_{2} P(x) \right) \mathrm{d}x \\ & = -\int_{x} P(x) \log_{2} Q(x) \mathrm{d}x - \left( -\int_{x} P(x) \log_{2} P(x) \mathrm{d}x \right) \\ & = H(P, Q) - H(P) \end{align*}

さらに, 相互情報量は, 同時確率分布から見た二つの確率分布の積とのKLダイバージェンスとして表せる :

I(X;Y)=DKL(P(x,y)∣∣P(x)P(y))I(X; Y) = D_{KL}(P(x, y) || P(x) P(y))

JS(Jensen-Shannon)ダイバージェンス

JSダイバージェンスでは, 対称性を持たなかったり, P(x)≠0,Q(x)=0P(x) \neq 0, Q(x) = 0 の領域で値が不定になったりするなどの問題点を持つKLダイバージェンスを改良して, 対称化・平滑化を行ったものであり, 次のように定義される :

DJS(P∣∣Q)=12DKL(P∣∣M)+12DKL(Q∣∣M)ただし, M=12(P+Q)(P, Qの混合分布)\begin{align*} D_{JS}(P || Q) & = \dfrac{1}{2} D_{KL}\left( P || M \right) + \dfrac{1}{2} D_{KL}\left( Q || M \right) \\ \text{ただし, } M & = \dfrac{1}{2} (P + Q) \quad \text{(P, Qの混合分布)} \end{align*}

JSダイバージェンスは, 次の特徴を持つ.

  • 常に 00 以上 11 以下の値を取り, P=QP = Q のときにのみ 00 となる.
  • 平滑性 : 極端な確率の差に対して穏やかな反応を示す.
  • 対称性 : DJS(P∣∣Q)=DJS(Q∣∣P)D_{JS}(P || Q) = D_{JS}(Q || P) が成り立つ(分布の順序に依存しない).
  • 有界性 : 常に有限の値を取る.

参考文献

関連記事

【E資格対策】パターン認識

【E資格対策】パターン認識

2026-02-05

E資格対策としてのパターン認識の備忘録です。「kd-tree」「近似最近傍」「コサイン距離」「ユークリッド距離」「マンハッタン距離」「Lp距離」「マハラノビス距離」の内容を含んでいます。

【E資格対策】パラメータ推定手法

【E資格対策】パラメータ推定手法

2026-02-05

E資格対策としてのパラメータ推定手法の備忘録です。「対数尤度」「最尤推定」「MAP推定」「ベイズ推定」の内容を含んでいます。