【E資格対策】性能指標

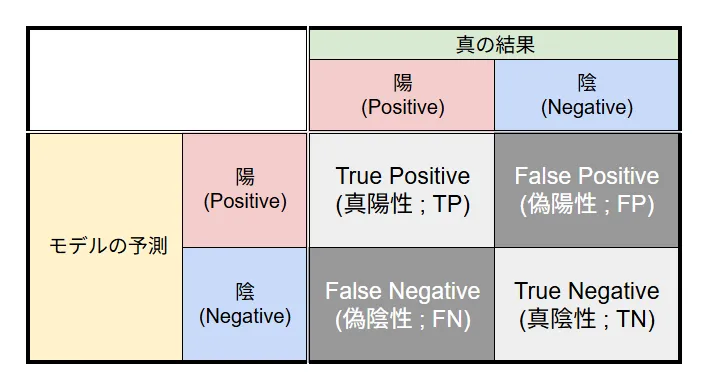
混同行列

混同行列は, 学習アルゴリズムの性能を明らかにする行列で, 機械学習の予測結果を理解し評価するために用いられる.

正解率・再現率・適合率・F値

不均衡なデータセットでモデルを評価する際は, 以下のような性能指標が有用である.

• 正解率(Accuracy) : 全予測に対する正しい予測の割合.
  • $\dfrac{TP + TN}{TP + TN + FP + FN}$
• 再現率(Recall, TPR) : 実際に陽性であるもののうち, 正しく陽性と予測された割合. 真陽性率とも.
  • $\dfrac{TP}{TP + FN}$
• 適合率(Precision) : 陽性と予測されたもののうち, 実際に陽性である割合.
  • $\dfrac{TP}{TP + FP}$
• F値 : 再現率と適合率の調和平均. 両者のバランスを評価する指標で, 双方が共に高い場合にのみ高い値を示す.
  • $\dfrac{2 \times (Recall) \times (Precision)}{(Precision) + (Recall)} = \dfrac{2TP}{2TP + FP + FN}$

代表的なものは以上であるが, 他にも様々な性能指標が存在する.

• 偽陽性率 : 実際に陰性であるもののうち, 誤って陽性と予測された割合.
  • $\dfrac{FP}{FP + TN}$
• 偽陰性率 : 実際に陽性であるもののうち, 誤って陰性と予測された割合.
  • $\dfrac{FN}{TP + FN}$
• 真陰性率(TNR) : 実際に陰性であるもののうち, 正しく陰性と予測された割合.
  • $\dfrac{TN}{FP + TN}$

ROC曲線・AUC

ROC曲線とAUC

ROC曲線(Receiver Operating Characteristic Curve) は, 性能に基づいて分類モデルを評価するための指標である. 縦軸に真陽性率(TPR), 横軸に偽陽性率(FPR) を取り, 分類器の可能な閾値全てに対して点をプロットし, それらを結んで曲線を描くことによって得られる.

理想的なモデルでは, 曲線が左端から上部を横断しグラフ領域全体を覆うようになり, FPRは $0$, TPRは $1$ となる.

また, ROC曲線の対角線はランダムな推定として解釈でき, 対角線を下回るモデルはランダムな推定よりも性能が劣ることを意味する.

AUC(Area Under the Curve) は, ROC曲線の下の面積を指し, 分類モデルの性能を数値で表すことができる.

AUCの値は $0$ から $1$ の範囲を取り, $1$ に近いほど優れたモデルであることを示す. また, AUCが $0.5$ の場合はランダムな推定と同等であることを意味する.

AUCの高いモデルは, FPRを低く保ちつつTPRを向上させる性能が優れている.

PR曲線との比較

PR曲線(Precision-Recall Curve)は, 分類モデルの性能を評価するためのもう一つの指標である. 縦軸に適合率(Precision), 横軸に再現率(Recall) を取り, 分類器の可能な閾値全てに対して点をプロットし, それらを結んで曲線を描くことによって得られる.

PR曲線は, 特に不均衡データセットにおいて有用である.

例えば, 正例が非常に少ないデータセットでは, ROC曲線の横軸である偽陽性率(FPR)が $0$ に非常に近い値を取ってしまう.

---

理由 (クリックで展開)

$(\text{FPR}) = \dfrac{FP}{FP + TN}$ であり, 多少の誤検出 $(FP)$ が発生しても $FP \ll TN$ となってしまうため, 分母が非常に大きくなり, 結果として $FPR \approx 0$ となる.

---

その結果, 「数値の上ではROC曲線は非常に優秀に見えるものの, 実態はボロボロ」というケースが起こりうる.

対して, PR曲線は分母に $TN$ を含まず,「陽性と予測したうち、どれだけ正解したか」にフォーカスするため, 不均衡データの実態を正確に反映することができる.

IoU・mAP

IoU(Intersection over Union)

IoUは, 物体検出タスクの精度を測定するための評価指標である.

IoUでは, 物体検出モデルによって提供される予測バウンディングボックス(予想領域)と, 実際に物体が存在する真のバウンディングボックス(正解領域)の重なり具合を評価する. 具体的には, 予想領域と正解領域の交差部分の面積を, 両者の和集合の面積で割った値として計算する.

IoUの値は $0$ から $1$ の範囲を取り, $1$ に近いほど予測が正確であることを示す.

※ 同一指標に「Jaccard係数」という二つの集合間の類似性を測定するものもある.

mAP(mean Average Precision)

AP(Average Precision)は, 物体検出タスクの精度を測定するための評価指標である.

APでは, 検出されたバウンディングボックスの中で正しいものの割合(適合率)と, 実際に存在するバウンディングボックスの中で正しく検出されたものの割合(再現率)を考慮する. 具体的には, PR曲線の下側の面積の総和として計算される.

APの値は $0$ から $1$ の範囲を取り, $1$ に近いほどモデルの精度が高いことを示す.

mAP(mean Average Precision)は, その名の通り, 各物体クラスごとのAPの平均値である.

APと同様に, mAPの値も $0$ から $1$ の範囲を取り, $1$ に近いほどモデルの精度が高いことを示す.

※ 詳しい説明は「【物体検出の評価指標】mAP ( mean Average Precision ) の算出方法 | Qiita 」を参照のこと。

micro平均とmacro平均

micro平均は, 多クラス分類問題において, 全クラスをまとめて計算する評価指標である.

サンプル数が多いクラスの予測結果が全体の評価に対して大きく寄与するため, 全体の性能を重視する場合に適している.

macro平均は, 多クラス分類問題において, 各クラスごとに計算した評価指標の平均値を取る方法である.

全てのクラスを平等に扱うため, 小数のサンプルしか持たないクラスも評価に等しく寄与する. そのため, 各クラスが同等に重要であると考えられる場合や, データの少ないクラスも重視したい場合に適している.

RMSE・MSE・MAE

この項では, $N$ をデータ数, $y_i$ を真の値, $\hat{y}_i$ を予測値とする.

• MAE(Mean Absolute Error, 平均絶対誤差) : 予測値と真の値の絶対誤差の平均. 外れ値の影響を比較的受けにくい.
  • $\text{(MAE)} = \dfrac{1}{N} \displaystyle \sum_{i=1}^{N} \left| y_i - \hat{y}_i \right|$
• MSE(Mean Squared Error, 平均二乗誤差) : 予測値と真の値の二乗誤差の平均. 外れ値の影響を受けやすいが, 逆に外れ値を重要視したい場合に有用でもある.
  • $\text{(MSE)} = \dfrac{1}{N} \displaystyle \sum_{i=1}^{N} \left( y_i - \hat{y}_i \right)^2$
• RMSE(Root Mean Squared Error, 二乗平均平方根誤差) : MSEの平方根. 目的変数の次元と同じになるため, 解釈が容易になる.
  • $\text{(RMSE)} = \sqrt{\dfrac{1}{N} \displaystyle \sum_{i=1}^{N} \left( y_i - \hat{y}_i \right)^2}$
    

他にも, 目的変数の変動(SST : Total Sum of Squares)に対して回帰モデルによって説明可能な割合を表す指標である 決定係数 $(R^2)$ がある. 一般に訓練データに対する決定係数は $0$ から $1$ の範囲を取るが, テストデータにおいては負の値もとり得る.

決定係数は以下のように計算される.

$$R^2 = 1 - \dfrac{\text{(SSE)}}{\text{(SST)}}$$

ここで,

• SSE(Sum of Squared Errors) 誤差平方和 : 予測値と真の値の差の平方和.
  • $\text{(SSE)} = \displaystyle \sum_{i=1}^{N} \left( y_i - \hat{y}_i \right)^2$
• SST(Total Sum of Squares) 総平方和 : 真の値と真の値の平均の差の平方和.
  • $\text{(SST)} = \displaystyle \sum_{i=1}^{N} \left( y_i - \bar{y} \right)^2$

である.

練習問題

問題1

ある病原体の検査薬を用いて, 感染者と思われる1000名に対して検査を行った. 予測結果と真の結果を比べ, 下表のような混同行列を作成して性能を評価した.

この結果について, 以下のうち最も適切な選択肢を1つ選べ.

$$\begin{array}{|c||c|c|} \hline & \text{結果 : 陽性} & \text{結果 : 陰性} \\ \hline\hline \text{予測 : 陽性} & 950 & 15 \\ \hline \text{予測 : 陰性} & 25 & 10 \\ \hline \end{array}$$

1. 再現率よりも適合率の方が高い.
2. 正解率は $97.4 \%$ である.
3. 真陰性率は $50 \%$ を超えており, 偽陽性率よりも低い.
4. 偽陰性率は $3 \%$ 未満であり,この値が低くなるほどモデルの性能が悪くなる.

---

解答 (クリックで展開)

順に吟味していく.

1. $(\text{再現率}) = \dfrac{950}{950 + 25} < \dfrac{950}{950 + 15} = (\text{適合率})$ より, 確かに適合率の方が高いので正しい.
2. $(\text{正解率}) = \dfrac{950 + 10}{1000} = 0.96 = 96 \%$ より, 誤り.
3. $(\text{真陰性率}) = \dfrac{10}{15 + 10} = 0.2857 \cdots < 0.5$ より, 誤り.
4. $(\text{偽陰性率}) = \dfrac{25}{950 + 25} = 0.0256 \cdots < 0.03$ であるが, 一般に偽陰性率が低くなるほどモデルの性能は良くなるので, 誤り.

よって, 正解は 1. である.

---

問題2

下表の混同行列(問題1と同じ)が表すF値を求めよ.

$$\begin{array}{|c||c|c|} \hline & \text{結果 : 陽性} & \text{結果 : 陰性} \\ \hline\hline \text{予測 : 陽性} & 950 & 15 \\ \hline \text{予測 : 陰性} & 25 & 10 \\ \hline \end{array}$$

---

解答 (クリックで展開)

$$\begin{align*} (\text{再現率}) & = \dfrac{950}{950 + 25} = 0.9743 \cdots \\ (\text{適合率}) & = \dfrac{950}{950 + 15} = 0.9844 \cdots \\ \end{align*}$$

であるから,

$$(\text{F値}) = \dfrac{2 \times 0.9743 \times 0.9844}{0.9743 + 0.9844} = 0.9793 \cdots \approx \underline{0.979}.$$

---

参考文献

• 深層学習教科書 ディープラーニング E資格（エンジニア）精選問題集